
Im Rahmen der Discounted Cash Flow Bewertung zinsen wir die prognostizierten Cash Flows der Zukunft mithilfe der Kapitalkosten auf den heutigen Zeitpunkt ab. Die Eigenkapitalkosten als Bestandteil der Gesamtkapitalkosten (WACC) berechnen wir dabei in vielen Fällen mithilfe des Capital Asset Pricing Modells (CAPM), für das der Faktor Beta einen wesentlichen Input darstellt.
Obwohl wir den Faktor in den meisten Fällen direkt von einer der bekannten Finanzwebseiten wie Yahoo Finance oder auch Finanzen.net abrufen können, sollten wir doch verstehen auf welcher Basis diese Zahlen entstehen… und warum wir sie vielleicht doch nicht einfach so verwenden sollten.
Was du in diesem Artikel lernst
- Wie der Beta-Faktor definiert ist
- Warum die Kennzahl als solche für unsere Bewertung problematisch ist
- Worin sich “Levered” und “Unlevered” Beta unterscheiden
- Welche alternativen Berechnungsansätze wir für die Abschätzung des Beta-Faktors nutzen können (Bottom-up Ermittlung auf Basis von Sektor-Betas etc.)
Beta Definition
Um den Faktor hinsichtlich der Definition von Risiko in der Portfoliotheorie besser zu verstehen, sollten wir zunächst einmal unterscheiden zwischen systematischen Risiken und unsystematischen Risiken.
Unsystematisches Risiko
Zu den unsystematischen Risiken gehören vor allem Firmen-spezifische Risiken wie z.B. die Überflutung einer Mine bei einem Minenbetreiber oder auch Managementfehler, Lieferengpässe, instabile Produktionsprozesse etc.
Unsystematische Risiken können – im Gegensatz zu systematischen Risiken – durch geschickte Diversifizierung, also ein Portfolio bestehend aus einer Bandbreite verschiedener Aktien, beseitigt werden.
Systematisches Risiko
Das systematische Risiko, oder auch Marktrisiko genannt, ist das Restrisiko, das auch bei ausreichender Diversifizierung theoretisch noch verbleibt. Also auch wenn wir also 10 Aktien oder mehr im Depot haben, dann sind wir diesem Risiko noch ausgesetzt. Es geht hierbei vor allem um Preisänderungen resultierend aus übergeordneten wirtschaftlichen Einflussfaktoren wie Zinsänderungen, Wirtschaftskrisen etc. Also Faktoren, die alle Aktien betreffen.
Die Theorie besagt außerdem, dass einzelne Aktien durch Änderungen dieser übergeordneten Faktoren stärker betroffen sind als andere.
Unternehmen wie Nestlé (NESN.VX) oder Coca Cola (KO) z.B. sollten auch durch stärkere wirtschaftliche Einbrüche nicht zu stark in Mitleidenschaft gezogen werden (essen und trinken müssen wir ja immer).
Im Gegensatz dazu sollten z.B. Automobilhersteller wie VW (VOW.DE) oder Daimler (DAI.DE) und Metallproduzenten / Minenbetreiber wie Rio Tinto (RIO) größere Krisen viel stärker spüren, weil die Nachfrage nach ihren Produkten dann viel stärker einbricht.
Beta
Der Beta-Faktor wurde nun entwickelt, um dieses systematische Risiko für einzelne Aktien im Vergleich zum Marktindex (also z.B. zum DAX oder zum S&P 500) abzubilden.
Hier die Beta-Definition des CFA Institute:
Beta is a measure of how sensitive an asset’s return is to the market as a whole. Beta captures an asset’s systematic risk, or the portion of an asset’s risk that cannot be eliminated by diversification. – CFA Institute
Ist eine Aktie z.B. als risikoreicher als der Markt einzustufen, dann ist der Beta-Faktor größer als 1. Ist eine Aktie weniger risikoreich, dann ist der Faktor kleiner als 1. Dies überträgt sich dann direkt in höhere bzw. niedrigere Kapitalkosten (Berechnung mit dem CAPM).
Es gibt übrigens auch Assets mit einem negativen Beta, was bedeutet, dass sich die Rendite gegenläufig zum Gesamtmarkt bewegt. Das war in der Vergangenheit z.B. für Gold so, weshalb viele Investoren Gold sozusagen als Portfolio-Absicherung im Depot hatten.
Cash hat ein Beta von ca. Null, d.h. der Wert bleibt konstant, egal in welche Richtung sich der Aktienmarkt ändert.
Beta-Faktor auf Finanzwebseiten
Wir können den Beta-Faktor im ersten Schritt entweder selbst berechnen oder direkt von einer Finanzwebseite wie Yahoo Finance oder Finanzen.net abrufen.

Wesentliche Kennzahlen Microsoft Corp.; Quelle: Yahoo Finance
Beta selbst berechnen
Statistisch gesehen ist Beta einfach das Ergebnis einer Regressionsanalyse der monatlichen Returns einer Aktie (z.B. Daimler) mit denen des Marktes (z.B. DAX), genauer gesagt die Steigung der resultierenden Regressionsgeraden:
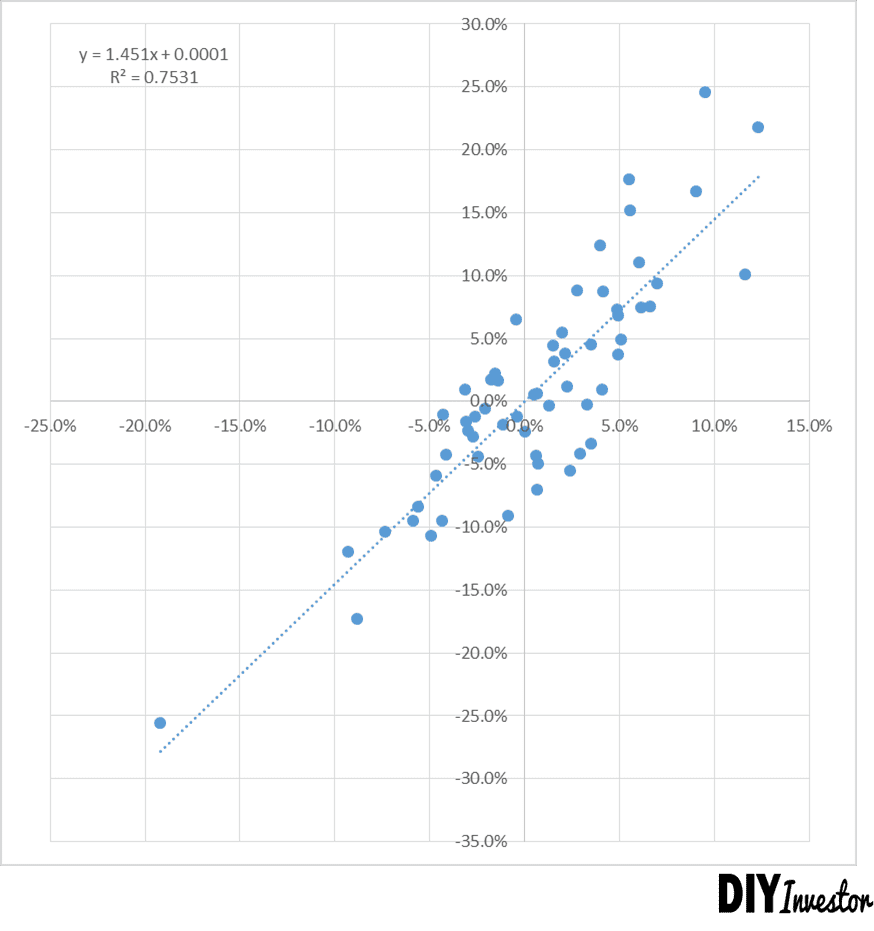
Regressionsanalyse Daimler vs. DAX
Auf der x-Achse sind die monatlichen Returns des Marktportfolios, in diesem Fall des DAX, abgetragen. Auf der y-Achse sehen wir die monatlichen Returns des betrachteten Einzelwertes, in diesem Fall Daimler. Für die Berechnung der Returns und des Regressions-Beta werden normalerweise die Schlusskurse der letzten 60 Monate genommen.
Anschließend wird einfach mithilfe von Excel eine Trendlinie durch die Datenpunkte gezogen (lineare Regression). Die Steigung dieser Geraden ist dann das Beta.
In diesem Fall liegt Beta bei 1,45, wie wir auch an der Formel der Regressionsgeraden im Chart erkennen können. Der Kurs der Daimler-Aktie scheint also im Vergleich zum DAX eine größere Schwankungsbreite zu haben. Wenn der DAX z.B. um 1% steigt oder fällt, dann steigt oder fällt die Daimler-Aktie im Mittel um 1,45% (und die von Microsoft um ~1,39% im Vergleich zum S&P 500). Diese größere Schwankung, also das höhere Beta, wird in der Theorie nun als risikoreicher angesehen.
Hier könnt ihr ein einfaches Excel-Tool herunterladen, mit dem ihr automatisch auf Basis der Yahoo Finance API das aktuelle Beta berechnen könnt!
Das hört sich ja eigentlich ganz einfach an.
Leider müssen wir aber doch noch eine Stufe tiefer ins Detail einsteigen, um den richtigen Faktor für unsere Kapitalkostenberechnung zu ermitteln.
Probleme mit dem Beta-Faktor
Es gibt da nämlich ein paar Probleme bzw. Schwierigkeiten mit dem Regressions-Beta, die ich euch nicht vorenthalten möchte.
Im Wesentlichen geht es dabei um Folgendes:
- der Beta-Faktor hängt stark vom zu Grunde gelegten Index ab
- die Regression zur Ermittlung des Beta-Faktors zeigt oft einen großen Standardfehler (Noise)
- der Faktor repräsentiert nicht den aktuellen Business Mix, sondern den historischen Mix der letzten fünf Jahre. Auch das Risiko des Cash-Bestandes (Beta ungefähr gleich Null) geht mit ein und kann über Zeit die Ergebnisse verfälschen
- der Faktor basiert auf der historischen und nicht der aktuellen bzw. prognostizierten Verschuldung
Warum Warren Buffett nichs von Beta hält: Hier nachlesen!
1. Abhängigkeit vom jeweiligen Index
Je nach dem, welchen Index wir der Regression zugrunde legen, kann ein größerer oder kleinerer Beta-Faktor herauskommen. Hier am Beispiel SAP (gelistet sowohl an der NYSE als auch in Frankfurt bzw. Xetra):

Die Analyse zeigt für SAP.DE versus dem DAX einen Faktor von 0,82, für SAP (NYSE) versus dem S&P 500 einen Faktor von 1,22. Die Unterschiede können also groß sein und unsere Abschätzung der Kapitalkosten signifikant beeinflussen.
2. Noise
Wir können den Beta-Faktor zwar für alle Aktien berechnen, in manchen Fällen ist er aber wenig aussagekräftig, weil die Returns der Aktie und des zugrunde gelegten Index offenbar gar nicht zusammenhängen (jedenfalls statistisch gesehen). Hier mal das Beispiel Amazon versus S&P 500:

Wir sehen im Wesentlichen nur eine Punktewolke und keinen schönen linearen Zusammenhang (höchstens mit etwas Fantasie). Am Beispiel SAP weiter oben sehen wir eigentlich das gleiche Phänomen.
3./4. Änderungen des Business Mix und der Verschuldung (Financial Leverage)
Weil das Beta auf Basis der monatlichen Returns der letzten fünf Jahre berechnet wird, basiert es natürlich auch auf den historischen Verschuldungsgraden sowie dem historischen Business Mix und Cash-Anteil.
D.h. wenn sich die Zusammensetzung oder der Verschuldungsgrad eines Unternehmens z.B. durch Akquisitionen oder Verkäufe in den letzten Jahren stärker geändert hat oder wir für die Zukunft von einer angepassten Kapitalstruktur ausgehen möchten, dann wird das im Beta nicht entsprechend reflektiert.
Alternative Ansätze für die Beta-Berechnung
Nun da wir um die Limitationen der standardmäßig verfügbaren Betas wissen, können wir diese eigentlich nicht mehr guten Gewissens für unsere DCF-Bewertung nutzen.
Das heißt wir brauchen einen alternativen Ansatz. Hier die verschiedenen Optionen laut Aswath Damodaran, Professor für Valuation an der NYU Stern School of Business:
- Wir modifizieren die Regression, indem wir den der Berechnung zugrunde liegenden Index ändern oder die Beta-Abschätzung mithilfe von fundamentalen Daten über das Unternehmen anpassen
- Wir schätzen das Beta für das Unternehmen über alternative Wege ab, indem wir einfach die Standardabweichung des Aktienkurses vom eigenen Mittelwert anstelle der Regression mit einem Marktindex nehmen oder die Returns auf Basis der veröffentlichten Gewinne und nicht der Marktpreise berechnen (weniger Noise)
- Oder wir ermitteln das Beta Bottom-up ohne die Zuhilfenahme einer Regressionsanalyse. Dafür müssen wir allerdings das Geschäft und die Produkte der Firma verstehen und den Verschuldungsgrad abschätzen können
- Alternativ können wir natürlich die Risikoprämie des Eigenkapitals ohne die Nutzung des Beta-Faktors abschätzen
Im Grunde genommen kommen für unsere Zwecke nur die Optionen 3 und 4 in Betracht. Die Option 3, also die Bottom-up Ermittlung des Beta-Faktors, möchte ich hier einmal im Detail erläutern.
Warum das Beta Bottom-up ermitteln?
Im Vergleich zur Nutzung des Regressions-Betas, wie wir es von Yahoo Finance etc. erhalten bzw. per Regression selbst berechnen können, liegt der große Vorteil einer Bottom-up Ermittlung darin, dass wir Anpassungen für Verschuldungsgrad, Cash-Anteil etc. selbst vornehmen können.
Das ist z.B. wichtig, wenn wir langfristig (also im DCF-Modell äquivalent zur Berechnung des Endwerts) von einer anderen Kapitalstruktur ausgehen, z.B. weil die Firma von der Wachstumsphase in die Reifephase des Lebenszyklus übergeht und deshalb ein anderes Risikoprofil bekommt.
Darüber hinaus sollte das Bottom-up ermittelte Beta einen um einiges geringeren Standardfehler aufweisen, weil wir mit einem Durchschnitt über eine größere Anzahl an Firmen arbeiten.
Beeinflussende Risikofaktoren
Bevor wir jedoch in die Details der Bottom-up Ermittlung abtauchen, sollten wir fürs Verständnis einmal kurz konzeptionell auf die verschiedenen, der Beta-Ermittlung zugrunde liegenden Risiken schauen.
Wie wir der folgenden Abbildung entnehmen können, gibt es im Wesentlichen drei firmenspezifische Faktoren, die das Beta beeinflussen.

Die Einflussfaktoren des Beta-Faktors; in Anlehnung an Damodaran
Da wäre zunächst mal das Produkt bzw. die Dienstleistung des Unternehmens. Je stärker die Konjunkturabhängigkeit eines Produktes oder einer Dienstleistung ist, desto stärker werden die Verkäufe in Folge einer Wirtschaftskrise zurückgehen. Wir sprechen hier also vor allem über Rohstoffe, Luxusgüter (Autos, Uhren, Schmuck) und andere hochpreisige Produkte. Es gibt also im weitesten Sinne eine Unterscheidung nach Industriesegment.
Der nächste Einflussfaktor ist das so genannte operative Leverage, also die Kostenstruktur des Unternehmens. Je höher der Anteil der Fixkosten an der Kostenstruktur, desto stärker wird der negative Effekt aus einem Rückgang der Produktionsmenge ausfallen, weil die Produktionskosten nur teilweise mit zurückgehen. Hohe Fixkosten bleiben natürlich erstmal einfach stehen und wir sehen in solchen Fällen sozusagen eine negative Fixkostendegression.
Schlussendlich spielt natürlich der Verschuldungsgrad bzw. das Financial Leverage eine wesentliche Rolle. Bei hoher Verschuldung kann eine Wirtschaftskrise ein Unternehmen schnell an den Rand der Pleite bringen. Nach der großen Übernahmewelle im Rohstoffsektor hatten z.B. viele Firmen in 2007 eine extrem hohe Verschuldung (und teilweise auch sehr kurzfristige Verbindlichkeiten), weil sie davon ausgingen, alles ganz easy aus dem hohen Cash Flow zahlen zu können. Als dann in 2008 die Krise kam und die Preise einbrachen, mussten viele Firmen entweder Notverkäufe tätigen oder sich von anderen übernehmen lassen, weil die Cash Flows massiv zurückgegangen waren.
Wie wir das Beta Bottom-up abschätzen
Der Beta-Faktor, den wir z.B. auf Yahoo Finance finden können, entspricht ungefähr dem Beta des Eigenkapitals ganz oben in der Abbildung bzw. dem so genannten “Levered” Beta (hierfür kenne ich leider keine deutsche Übersetzung). Einziger Unterschied ist die Berücksichtigung des Cash-Bestandes, der natürlich in den Yahoo Finance Daten enthalten ist (weil die Daten ja auf den realen Returns basieren).
Den Cash-Bestand bzw. das Risiko des Cash-Bestandes würden wir für die Bottom-up Ermittlung natürlich nicht berücksichtigen, weil uns nur das Risiko des operativen Geschäfts interessiert (welches wir später mithilfe des DCF-Modells bewerten).
Für die Bottom-up Ermittlung des Betas würden wir entlang der folgenden drei Schritte vorgehen:
- Wir ermitteln zunächst ein Sektor-spezifisches Beta korrigiert um die Kapitalstruktur und den Cash-Anteil (der ja ein Beta von ca. Null haben sollte)
- Dann passen wir dieses Beta auf Basis des operativen Leverage, also des Fixkostenanteils, an (und erhalten das “Unlevered” Beta des Unternehmens)
- Abschließend berechnen wir mithilfe des Verschuldungsgrades (bzw. Financial Leverage) das Beta des Eigenkapitals (“Levered” Beta)
Hört sich erstmal kompliziert an, ist aber bei genauem Hinsehen gar nicht so schwierig.
1. Sektor-spezifische Betas
Den Ausgangspunkt für unsere Bottom-up Ermittlung bilden die Industrie-spezifischen Betas. Für deren Ermittlung werden einfach Regressions-Betas einer Reihe von Firmen eines bestimmten Sektors (z.B. für den Automobilsektor Europa bestehend aus VW, Daimler, BMW, Fiat Chrysler, PSA etc.) gemittelt.
Anschließend wir der resultierende Beta-Faktor, der ja auf der durchschnittlichen Kapitalstruktur des Sektors (bzw. der Firmen, die wir für die Berechnung des durchschnittlichen Betas ausgewählt hatten) basiert, nochmal entsprechend korrigiert.
Die Effekte aus der Kapitalstruktur werden also herausgerechnet. D.h. wir tun erstmal so, als wären alle Firmen nur mit Eigenkapital finanziert. Das Risiko wird dann entsprechend niedriger. Genauso wie das Sektor-Beta. Praktisch gesehen berechnen wir das “Unlevered” Sektor-Beta mit der folgenden Formel:
“Unlevered” Sektor-Beta = Sektor-Beta / (1 + (1- Steuersatz) * (Debt/Equity Ratio des Sektors))
Dieser Beta-Faktor ist zwar bereits korrigiert um den Verschuldungsgrad der Industrie bzw. des Sektors. Allerdings ist der Wert nach wie vor ein Mittelwert, nämlich aus dem durchschnittlichen Beta des operativen Geschäfts und dem durchschnittlichen Beta des Barmittelbestandes (Cash) der Industrie bzw. des Industriesektors.
Für unsere Bewertung nach der DCF-Methode interessiert uns allerdings nur der betriebliche Teil des Business, also das operative Geschäft. Die Barmittelbestände brauchen wir nicht zu bewerten, weil wir den Wert natürlich bereits kennen. Dem entsprechend korrigieren wir das Sektor-Beta noch um diese Barmittelbestände.
Und zwar folgendermaßen: Weil Cash bzw. Cash Äquivalente ein Beta von ungefähr Null haben sollten (d.h. der Wert des Cash bleibt immer mehr oder weniger konstant, unabhängig davon, was der Markt macht), können wir das “Cash-adjustierte” Beta einfach aus dem bereits berechneten “Unlevered” Beta und dem Cash-Anteil am Firmenwert ableiten:
“Cash-adjustiertes” Beta = “Unlevered” Beta / (1 – Cash / Firmenwert)
Wenn also das “Unlevered” Beta für eine ganze Firma bei 1,20 liegt und der Cash-Anteil 20% beträgt, dann berechnen wir den “Cash adjustierten” Faktor einfach zu 1,50 = 1,20 / ( 1 – 20%).
Glücklicherweise müssen wir alle diese Kalkulationen nicht selbst machen, sondern können uns aus bereits existierenden Daten bedienen. Aswath Damodaran hat nämlich für seine Studenten entsprechende Excel-Files mit einer langen Reihe an Industrien zusammengestellt, die für alle zum Download verfügbar sind (klick auf die Abbildung zum Download des Excel-Files):

Auszug Sektor-Betas (“Levered” und “Unlevered”); Quelle: Aswath Damodaran
Ist übrigens eine Firma in mehreren Industrie-Sektoren oder -segmenten tätig (was ja keine Seltenheit ist, siehe z.B. Siemens), dann sollten wir ein entsprechend gewichtetes Beta berechnen.
2. Anpassung für operatives Leverage
Wenn eine Firma in einer bestimmten Industrie bzw. in einem bestimmten Sektor oder Business prozentual gesehen hohe Fixkosten hat, dann ist sie höheren Risiken ausgesetzt als eine vergleichbare Firma mit geringem Fixkostenanteil.
Wenn wir also auf Basis der Financials eine Einteilung der Kosten in fix und variabel vornehmen können, dann sollten wir das Sektor-Beta nach folgender Formel anpassen:
“Unlevered” Beta Firma = “Unlevered” Sektor-Beta * (1 + (Fixkosten / Variable Kosten))
Hat eine Firma gar keine Fixkosten, dann bleibt das Beta wie es ist. Hat eine Firma Fixkosten und variable Kosten in gleicher Höhe, dann verdoppelt sich das Beta. Beide Fälle sind natürlich rein theoretisch.
In den meisten Fällen (wahrscheinlich 99% der Fälle) wird eine Einteilung der Kosten in fixe und variable allerdings nicht ohne Weiteres möglich sein. In der Praxis wird deshalb oft angenommen, dass die Fixkostenanteile aller Firmen in einer Industrie in etwa gleich sind und es wird keine Anpassung des Sektor-Betas für operatives Leverage vorgenommen.
3. Anpassung für Financial Leverage bzw. Verschuldungsgrad
Der letzte Schritt auf unserem Weg zum Beta für unsere DCF-Bewertung bzw. die Berechnung der Eigenkapitalkosten ist die Berücksichtigung des Verschuldungsgrades bzw. des Financial Leverage der Firma.
Hier die Formel:
“Levered” Beta = “Unlevered” Beta * ( 1 + (1- Steuersatz) * (Debt/Equity Ratio)))
Manchmal wird übrigens der positive Steuereffekt der Schulden auch außen vor gelassen und der entsprechende Teil der Formel entfällt. Das hier verwendete Debt-to-Equity Ratio basiert übrigens auf dem Marktwert des Eigenkapitals (also der Marktkapitalisierung = Aktienkurs * Umlaufende Aktien) und dem Buchwert der langfristigen und kurzfristigen Finanzschulden (also ohne Berücksichtung von Verbindlichkeiten aus L.u.L. und anderer nicht-zinstragender Schulden).
Beispiel: Bottom-up Beta für Microsoft
Die folgende Tabelle enthält die Berechnung des Beta am Beispiel Microsoft (MSFT):

Gehen wir einmal im Einzelnen durch:
Alle relevanten Informationen zum Sektor-Beta können wir aus dem Excel von Aswath Damodaran entnehmen (in der Tabelle gelb hinterlegt). Daraus können wir dann nach wie oben beschrieben zunächst das “Unlevered” Beta berechnen.
Im Fall MSFT habe ich hier den Sektor “Software (Systeme und Applikationen)” verwendet. Das angepasste Sektor-Beta (also korrigiert um Sektor-Verschuldung und -Cash) beträgt in diesem Fall 0,99.
Eine Anpassung für operatives Leverage habe ich nicht vorgenommen.
Das Debt-to-Equity Ratio für Microsoft habe ich auf Basis der aktuellen Marktkapitalisierung (ca. 495 Mrd. USD) und den durchschnittlichen Schulden der letzten zwei Geschäftsjahre (ca. 44 Mrd. USD) berechnet. Damit erhalten wir ein Debt-to-Equity Ratio von ca. 9%
Zusammen mit dem aktuellen durchschnittlichen Steuersatz von rund 15% ergibt sich für MSFT ein Beta von 1,07, also signifikant niedriger als 1,39, der Wert, den wir aus Yahoo Finance entnehmen können und den nebenbei auch andere Finanzwebseiten wie z.B. Gurufocus für die Berechnung der Kapitalkosten nutzen.
Fazit
Das von Finanzwebseiten wie Yahoo Finance verfügbare Beta wird auf Basis einer Regression der historischen Returns der Aktie mit den Returns eines Index (z.B. des DAX) ermittelt.
Aus diesem Grund haben wir mit diesem Faktor die gleichen Probleme, die wir auch bei anderen Regressionsanalysen haben:
- Noise
- Abhängigkeit vom verwendeten Index und vom betrachteten Zeithorizont
- historische Gegebenheiten, die sich inzwischen stark geändert haben könnten (in diesem Fall Kapitalstruktur, Cash-Anteil etc.)
Als Alternative können wir das Beta z.B. Bottom-up auf Basis von Sektor-Betas berechnen. Dies hat den Vorteil, dass wir den Cash-Anteil direkt bereinigen und den Einfluss der Kapitalstruktur (Financial Leverage) individuell einstellen können.
Darüber hinaus sollte das Sektor-Beta als Ausgangspunkt aufgrund der breiteren Zahlenbasis signifikant weniger Noise aufweisen.
Mit den Sektor-Daten als Ausgangspunkt ist die Ermittlung des Betas auch nicht viel aufwendiger als die Nutzung des Regressions-Beta von Yahoo Finance. Ich würde daher standardmäßig den Bottom-up Ansatz wählen.
Oder was meint ihr? Nutzt ihr Beta überhaupt? Kommentiert einfach unten oder schreibt mir eine Email.
2 Kommentare zu „Beta: Wie wir die Kennzahl richtig abschätzen“
Hi,
Ich nutze das Beta nie. Und habe es bis heute nicht gebraucht. Für Portfoliomanager bzw. Fondmanager großer Fonds sehe ich den Vorteil ein Portfolio schwankungsärmer zu gestalten, was für viele Kunden sicher enorm wichtig ist. Die Kunden würden bei einem stärken Einbruch schnell Gelder abziehen…
Bei mir im Portfolio muss ich das nicht tun. Ich investiere nach anderen Faktoren. Wer weiß, was für systematische Risiken ich schon in meinem Portfolio hatte… 😀
Wenn du ein unterbewertetes Unternehmen findest, wo dich Produkt und Management auch noch begeistern, schaust du dann wirklich auf systematische Risiken? Für mich steht der Beta irgendwie schon fast im Kontrast zu Value Investing Techniken, wo du nach ganz anderen Kriterien dein Risiko nach unten verringerst. Oder bist du anderer Meinung?
Nutzt du denn das Beta?
Alles Gute,
Ferhat
Hi Ferhat,
danke dir für dein Feedback! Ich bin ganz deiner Meinung. Als Value Investoren interessieren wir uns ja typischerweise für gut vorhersehbare und leicht verständliche Geschäftsmodelle und können in solchen Fällen deshalb mit einem anderen Ansatz wie langfristige Bondrate plus ein paar Prozentpunkte (und dann einer hohen Sicherheitsmarge) arbeiten.
Ich versuche mich dem Ganzen auf mehreren Wegen zu nähern und berechne deshalb u.a. auch das Beta bzw. die Eigenkapitalkosten mithilfe des CAPM als Vergleichswert, um zu sehen, wo ich damit landen würde (bzw. was die Erwartung des Marktes ist).
Cheers,
Axel