Vor einiger Zeit hatte ich mich einmal mit dem theoretischen Fundament der so genannten Kelly-Formel bzw. des so genannten Kelly-Kriteriums beschäftigt, einem Hilfsmittel, welches von einigen wenigen Value Investoren (nachweislich Mohnish Pabrai, Bill Miller, Nick Sleep) zur Ableitung von Positionsgrößen im Portfolio verwendet wird bzw. verwendet wurde.
Dabei denke ich ist es kein Zufall, dass genau die angesprochenen Investoren tendenziell eher stark konzentrierte Portfolios managen bzw. in der Vergangenheit gemanagt haben. Wie einigen vielleicht bekannt, hatte die Nomad Partnership zum Zeitpunkt ihrer Auflösung im Jahr 2011 nur ganze drei Aktien im Portfolio (Costco, Amazon, Berkshire).
In diesem Artikel möchte ich nun einmal auf ein paar ganz praktische Aspekte des Kelly-Kriteriums eingehen… und eine noch weiter vereinfachte Version der Kelly-Formel vorstellen.
Intro: Diversifikation versus Konzentration
Zum Einstieg mal ein kleines Gedankenexperiment (übernommen aus einem der Partnership-Letter von Nick Sleep / Nomad): Theoretisch – also sofern wir sie denn finden – könnten wir 50 sehr attraktive Investmentideen mit identischer Sicherheitsmarge und identischer Wertrealisierungswahrscheinlichkeit über die Zeit (= Überzeugung bzw. Conviction) in unserem Portfolio ganz stupide einfach gleich gewichten (d.h. jeder Wert bekommt einen Portfolioanteil i.H.v. 2%).
Neben der attraktiven Wertsteigerung wäre ein solches Portfolio aufgrund der starken Diversifikation (50 Werte!) im relativen Vergleich zu einem stark konzentrierten Portfolio mutmaßlich sehr schwankungsarm (heißt es hätte eine geringe Volatilität)
Natürlich sind diese “besten” Ideen in der Praxis sehr selten. Wenn man den erfolgreichsten Investoren in dieser Hinsicht Glauben schenken darf, dann kann man von Glück sagen, wenn man dazu in der Lage ist, auch nur eine oder zwei solcher Ideen pro Jahr zu identifizieren… was natürlich die Frage aufwirft, welchen Anteil des Kapitals man eigentlich in jede dieser seltenen Ideen investieren sollte.
An dieser Stelle kommt das Kelly-Kriterium ins Spiel (im Folgenden nur eine kurze Rückschau. Für mehr Details schaut euch einmal den ursprünglichen Beitrag zum Thema Kelly an).
Recap: Das Kelly-Kriterium im Investment-Kontext
Das Kelly-Kriterium (nach John Kelly, 1956) berechnet den Anteil des Kapitals, der idealerweise eingesetzt werden sollte, um langfristig das Portfolio-Wachstum zu maximieren. Die Formel lautet in einfacher Form:
Kelly-% = Edge / Odds („Erwartungswert“ / möglicher Gewinn)
Kleines Beispiel Münzwurf: 50%ige Gewinnchance pro 1 EUR Einsatz (heißt Erwartungswert gleich 0,5 EUR), möglicher Gewinn = 2 EUR, also Kelly-% = 0,5 / 2 = 25%
Viele renommierte Investoren wie Warren Buffett, Mohnish Pabrai oder Joel Greenblatt haben (bewusst oder intuitiv) entsprechend des Kelly-Kriteriums investiert: Mithilfe konzentrierter, aber wohl überlegter Portfolioallokationen.
Die Limitationen der Kelly-Formel für die Anwendung im Investment-Kontext auf der anderen Seiite sind aber auch klar: Die Formel setzt Wiederholbarkeit (n-fache identische Wetten) voraus und ist daher bei Einmal-Investments schwieriger anzuwenden… bzw. jedenfalls um einiges schwerer nachzuvollziehen (weshalb vermutlich auch Mohnish Pabrai sich irgendwann wieder etwas von der Formel distanziert hat).
Um diesen Aspekt nochmal zu illustrieren (anhand des obigen, einfachen Beispiels): Man setzt zunächst 25% des Kapitals auf ein Investment mit einer 50%igen Gewinnchance und 200% Wertsteigerungspotenzial. Verliert man im ersten Schritt, setzt man 25% des verbliebenen Kapitals auf die gleiche Wette… usw.
Statistisch gesehen müsste man in der langen Frist zwar jede zweite Wette gewinnen. Das bedeutet allerdings noch nicht, dass man nicht auch mal zwei oder drei Wetten infolge verlieren und so sein Kapital stark in Anspruch nehmen kann.
Die Kelly-Formel balanciert nun Wachstum und Risiko so aus, dass das langfristige Kapitalwachstum maximiert wird:
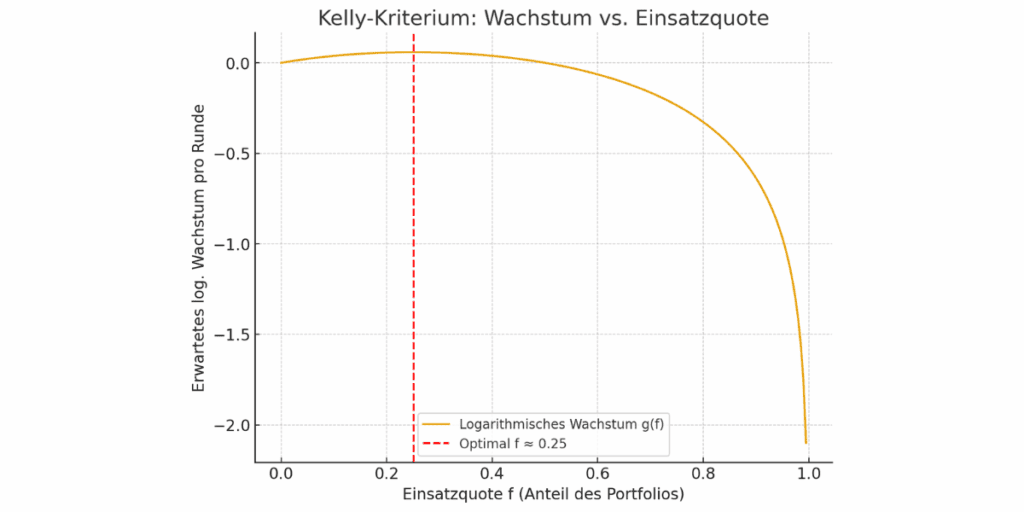
Wie ihr der obigen Grafik entnehmen könnt, stellt eine Wette von „nur“ 25% in diesem Fall die optimale Lösung dar. Die langfristige Wachstumsrate wird auf diese Weise maximiert:
- Zu hohe Einsätze steigern kurzfristig das Risiko eines Totalverlustes unverhältnismäßig stark, obwohl das Chance-Risiko-Verhältnis ganz allgemein sehr zu Gunsten der Wette ausgelegt ist
- Zu geringe Einsätze hingegen mindern das Wachstumspotenzial und führen nur zu unterdurchschnittlichen Returns
Also kurz gesagt: Kelly ist im Grunde genommen ein mathematischer Schutz vor “Overbetting”, aber auch vor “Overdiversification”.
Praktische Implikationen aus der Nutzung der Kelly-Formel
Der wesentliche Punkt aus Investorensicht ist allerdings: Das Kelly-Kriterium funktioniert eher sequentiell (n Durchläufe einer identischen Wette) und berücksichtigt daher nicht die vielen anderen Restriktionen, die mit der Konstruktion eines Wertpapierportfolios typischerweise einhergehen.
Darüber hinaus führt die Anwendung des Kelly-Kriteriums in vielen Fällen zu sehr aggressiven Einsätzen, zu Wetten also, die im Grunde genommen nur die wenigsten Investoren einzugehen bereit sein werden.
Was beobachten wir also in der Praxis? Zunächst mal schrieb Nick Sleep in 2004:
But does anyone do that? As far as we are aware, only the early Buffett Partnership portfolios had anywhere near this level of concentration, and then mainly in companies in which Buffett was a controlling shareholder. – Nick Sleep (2004)
Außer Warren Buffett’s erster Partnership hatte also nach seinem Wissensstand niemand auch nur annähernd eine so hohe Konzentration von Einzelwerten im Portfolio. Und selbst Buffett ging tendenziell nur “all-in”, wenn er gleichzeitig als “Controlling Shareholder” auch großen Einfluss nehmen konnte (also vollen Durchgriff auf das Management des Unternehmens hatte).
Nichts desto trotz sagt Sleep, dass Kelly im Grunde genommen den richtigen Ansatz darstellt, wenn es um das Thema Portfoliokonstruktion geht. Auf Basis der vorhandenen Informationen scheint er das Konzept allerdings eher angewendet zu haben, um für eine relativ hohe Portfoliokonzentration zu argumentieren (und nicht so sehr, um die Gewichtung von Einzelwerten zu bestimmen):
If you know you are right, why would you not bet a high proportion of the portfolio in that idea? The logical extension of this line of thought is that Nomad’s portfolio concentration has at times been too low. And if it has been too low at Nomad, what has been going on at the large mutual fund complexes with many hundred stocks in a single country portfolio? Apply the Kelly criterion, and the average fund manager would appear to have almost no clue as to the likely success of any one idea. In our opinion, the massive overdiversification that is commonplace in the industry has more to do with marketing, making the clients feel comfortable, and the smoothing of results than it does with investment excellence. At Nomad we would rather results were more volatile year to year but maximized our rolling five-year outcome. If you do not share this view, think long and hard about your investment in Nomad. – Nick Sleep (2004)
Nach meinem Dafürhalten erscheint diese Denkweise in der Tat sehr sinnvoll zu sein. Denn wer generell nur ca. 10-20 Werte im Portfolio zulässt (oder sogar noch weniger), der muss bei jedem einzelnen Wert dafür sorgen, dass es sich um ein hochattraktives Investment mit geringem Verlustrisiko handelt.
Und umgekehrt: Wer sehr von einem Investment überzeugt ist, sollte auch einen substanziellen Anteils seines Kapitals auf dieses Investment allokieren können.
Was uns allerdings noch nichts darüber verrät, wie wir Kelly tatsächlich in der Praxis anwenden können.
Mögliche Anpassungen des Kelly-Kriteriums
Aus Sicht eines Praktikers besteht der zentrale Kritikpunkt am Kelly-Kriterium darin, dass die Formel oft sehr aggressive Gewichtungen liefert, weil sie davon ausgeht, dass Wahrscheinlichkeiten und Auszahlungen exakt bekannt sind. In der Realität handelt es sich allerdings meist nur um grobe Schätzungen.
Daher haben findige Investoren im Laufe der Zeit ein paar gängige Abschwächungen des Kelly-Kriteriums (bzw. Schutzmechanismen) entwickelt:
- “Fractional Kelly” / “Half Kelly”
- Cap auf maximale Positionsgrößen
- Anpassung der Wahrscheinlichkeiten („Kelly mit Margin of Safety“)
- Kelly als Ranking-Tool, nicht als harte Regel
- …
Im Folgenden einmal eine Kurzübersicht der möglichen Kelly-Anpassungen für die Praxis.
Hinweis: Natürlich lassen sich die dargestellten Abschwächungen auch miteinander kombinieren. Mir beispielsweise erscheint eine Anwendung von “Half Kelly” kombiniert mit einem Cap auf die maximale Positionsgröße ein passender Ansatz zu sein.
“Fractional Kelly” / “Half Kelly”
Anstatt den vollen Kelly-Anteil zu allokieren, investiert man z.B. nur die Hälfte (“Half Kelly”) oder ein Viertel dessen, was mithilfe der Kelly-Formel errechnet wurde.
Dieses Vorgehen reduziert die Volatilität und schützt darüber hinaus vor Fehlern in den Annahmen.
Und: Selbst Half Kelly erreicht – bei einem deutlich geringeren Risiko – in den meisten Fällen ~70-80% der langfristigen Wachstumsrate.
Tatsächlich nutzen viele Hedgefonds-Manager und Trader “Half Kelly” als Standard zur Bestimmung ihrer Positionsgrößen:
If you bet half the Kelly amount, you get about three-quarters of the return with half the volatility. So it is much more comfortable to trade. I believe that betting half Kelly is psychologically much better. – Hedgefonds-Manager in Hedge Fund Market Wizards
Cap auf maximale Positionsgrößen
Unabhängig von der Kelly-Berechnung legt man eine harte Obergrenze für Einzelpositionen fest (z.B. max. 15-20% pro Aktie).
Mit diesem Vorgehen verhindert man extreme Konzentration bei vermeintlich „sicheren“ Chancen, die sich später u.U. als Fehleinschätzungen herausstellen können.
„Kelly mit Margin of Safety“
Anstatt zu optimistische Wahrscheinlichkeiten oder Payoffs anzusetzen, verwendet man eher defensive bzw. konservative Inputs bzgl. der Gewinnwahrscheinlichkeit (niedriger ansetzen) und / oder der Gewinnhöhe (ebenfalls niedriger ansetzen).
Im Ergebnis erhält man konsequenterweise weniger extreme bzw. konservativere Kelly-Empfehlungen.
Kelly als Ranking-Tool, nicht als harte Regel
Viele Investoren nutzen Kelly eher als Signalstärke-Maßstab (große Kelly-Werte = starke Überzeugung), ohne aber die Empfehlung 1-zu-1 umzusetzen. So dient Kelly als Priorisierungs-Tool, nicht aber als starres Gewichtungssystem.
Vereinfachte Version der Kelly-Formel
Dieser Absatz ist eher informatorischer Natur: Nick Sleep nutzte für die in seinen Investorenbriefen dargestellten Kelly-Berechnungen eine etwas vereinfachte Version der Kelly-Formel (ich habe etwas Zeit in die Suche nach einer weiteren Referenz investiert, tatsächlich aber nur die Erwähnung im Nomad Shareholder Letter aus 2004 gefunden).
Die Formel kommt ohne eine Einschätzung des Wertsteigerungspotenzials aus und erfordert als einzige Variable die Gewinnwahrscheinlichkeit (i.W. gleichzusetzen mit unserem Grad an Überzeugung):
Gewichtung Investment = 2,1 x Gewinnwahrscheinlichkeit – 1,1
Also Beispiel: Sind wir uns zu 75% sicher, dass ein Investment erfolgreich sein wird, dann sollten wir entsprechend der vereinfachten Kelly-Formel ca. 47,5% des Kapitals in die Idee investieren.
Gewichtung = 2,1 x 75% -1,1 = 0,475 = 47,5%
Ich denke es hängt etwas vom Anwendungsbereich ab, welche Version der Kelly-Formel wir konkret für unsere Analysen verwenden. Ich persönlich würde für die Anwendung der oben dargestellten ursprünglichen Variante votieren, weil gerade Wertsteigerungspotenzial sich je nach Investment stark unterscheiden kann.
Bottom Line
Während die Manager stark diversifizierter Portfolios ihren Fokus auf die Reduktion von Volatilität legen, haben erfolgreiche Investoren wie Warren Buffett, Mohnish Pabrai oder Nick Sleep über lange Zeiträume immer wieder bewiesen, dass hochkonzentrierte Portfolios auf Basis der “besten” Ideen den Markt nachhaltig outperformen können.
Die klassische Kelly-Formel berechnet nun den optimalen Kapitaleinsatz bzw. die optimale Portfolioallokation basierend auf Gewinnwahrscheinlichkeit und möglichem Gewinn, führt allerdings auch oft zu sehr aggressiven Gewichtungen.
Praktische Anpassungen wie “Fractional Kelly” bzw. “Half Kelly”, Caps auf Positionsgrößen, konservative Wahrscheinlichkeiten oder die Nutzung als Ranking-Tool können uns dabei helfen, Risiko und Volatilität zu reduzieren. Also zusammenfassend:
- “Voll Kelly” maximiert mathematisch das Wachstum, ist aber oft realitätsfern und riskant
- “Half Kelly” + Positionslimits + konservative Annahmen ist die gängigste Praxis unter Profis
- Kelly ist wertvoll als Rahmen für diszipliniertes Risiko- und Positionsgrößenmanagement, aber selten 1-zu-1 in Reinform nutzbar